Lesson 3	Converting binary to Decimal
Objective	Convert numbers between binary and decimal form.

Conversion Between Binary and Decimal Numbers

Binary and decimal are two different number systems. The decimal system, also known as the base-10 system, is what we use in everyday life and consists of ten digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. The binary system, or base-2 system, consists of just two digits: 0 and 1. Computers inherently use the binary system due to their digital electronic nature.

Converting Decimal to Binary:
Division by 2 Method
To convert a decimal number to its binary equivalent, follow these steps:
1. Divide the decimal number by 2.
2. Record the remainder. This will be the least significant bit (LSB).
3. Use the quotient from the previous division as the new number to be divided.
4. Repeat the process until the quotient becomes zero.
5. The binary equivalent is the sequence of remainders read from bottom (last remainder) to top (first remainder).
Example: Convert 13 (decimal) to binary.
```
13 ÷ 2 = 6 remainder 1  <- LSB
6 ÷ 2 = 3 remainder 0
3 ÷ 2 = 1 remainder 1
1 ÷ 2 = 0 remainder 1  <- MSB
```
Reading from the MSB to the LSB, 13 in decimal is equivalent to 1101 in binary.
Converting Binary to Decimal:
To convert a binary number to its decimal equivalent, follow these steps:
Positional Weight Method:
1. Write down the binary number and assign a positional weight to each bit, starting from the rightmost bit (LSB) as 2^0 and increasing by one power of 2 for each position to the left.
2. Multiply each bit by its positional weight.
3. Sum the results of these multiplications.
Example: Convert 1101 (binary) to decimal.
```
(1 × 2^3) + (1 × 2^2) + (0 × 2^1) + (1 × 2^0)
= 8 + 4 + 0 + 1
= 13
```
Thus, 1101 in binary is equivalent to 13 in decimal.

Understanding the conversion between binary and decimal systems is fundamental in computer science, as it bridges the gap between human-readable numbers and the binary language of computers. Mastery of these conversions equips one with the foundational knowledge required for various computer operations and algorithms.

Converting a binary number to its decimal equivalent is fairly straightforward. Simply add the powers of 2 corresponding to the positions of the 1s in the binary number. For your reference, here are the first 8 powers of 2.

2⁷	2⁶	2⁵	2⁴	2³	2²	2¹	2⁰
128	64	32	16	8	4	2	1

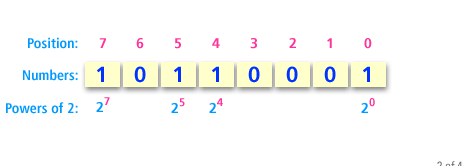
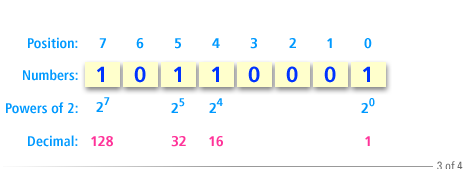
The following series of images shows how to convert the binary number 10110001 to its decimal equivalent.

Converting between binary and decimal

1) The following sequence outlines the steps in converting the binary number 10110001 to decimal equivalent. — 1) The following sequence outlines the steps in converting the binary number 10110001 to its decimal equivalent.

2) The 1st in this binary number are the positions corresponding to 2 raised to the 7th, 2^5, 2^4, 2^0

3) Calculate the decimal equivalent of each power of 2 (i.e. 2^7 = 128)

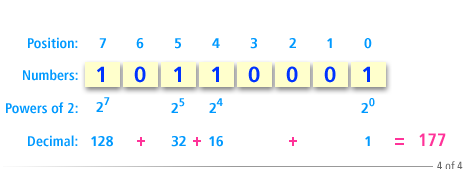
4) Add the decimal equivalent of each power of 2. The total is the decimal value of the binary number.
128 + 32 + 16 + 1 = 177